[Excelにおける回帰分析 (1)最小二乗法の発想] 
Excel(エクセル)における回帰分析の手順と出力の意味を説明します。
このページでは、回帰分析とも言われる最小二乗法の発想について説明します。
Excelにおける回帰分析(最小二乗法)用乱数データ:乱数を用いて、推定値の挙動を見ることのできるExcel(約100KB)です。
分散の不偏推定量:偏差平方和を(n-1)で割ると分散の不偏推定量になることが視覚的に確認できるExcel(約80KB)です。
中心極限定理と擬似正規乱数:一様分布の標本平均が正規分布に近づくことや統計における検定のアイディアが視覚的に確認できるExcel(約60KB)です。
学校は人的資本を形成するのか? (1)教育の経済学:分布やシミュレーションを使って、学歴と平均賃金の関係を説明するHTMLです。
学校は人的資本を形成するのか? (2)賃金格差の実証分析:日本の学歴間賃金格差の実証分析を説明するHTMLです。
目次 : このページから始まるExcelにおける回帰分析では、Microsoft(マイクロソフト)のExcel(エクセル)における回帰分析の手順と出力の意味を説明します。予備知識がない方であっても、Excel の分析ツールを使って回帰分析の結果を出せるようになります。また、回帰分析の性質、統計量の意味、実証分析を行う上での注意点が書いてあります。
1.1 差分の二乗和を最小化
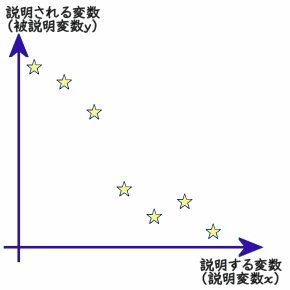
左下図のような説明する変数(説明変数)![]() と説明される変数(被説明変数)
と説明される変数(被説明変数)![]() があるとします。説明変数
があるとします。説明変数![]() ⇒被説明変数
⇒被説明変数![]() の効果の大きさを調べたり、予測をしたりするために関係を示す直線を引くことを考えます。
の効果の大きさを調べたり、予測をしたりするために関係を示す直線を引くことを考えます。![]() として、切片の高さ
として、切片の高さ![]() や傾き
や傾き![]() を動かして、当てはまりの良い直線を考えます。
を動かして、当てはまりの良い直線を考えます。
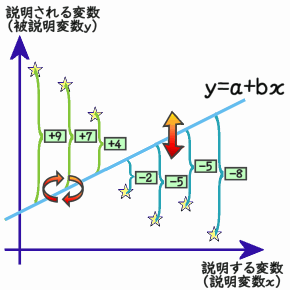
単純に考えれば、星と線の差分の距離が小さくなるように線を引くと、当てはまりが良さそうです。しかし、差分の総和を最小化すると、右下図のようにプラスとマイナスが相殺することがあります。また、星のずっと上の方に線を引けば、差分の総和は絶対値の大きなマイナスの値をとることができます。よって、差分の総和の最小化では当てはまりの良い線は引けません。当てはまりの良い線を引く一つの方法は『差分の二乗』の総和を最小化する最小二乗法です。回帰分析とも言われる最小二乗法は、二乗することで全ての差分をプラスにしてから総和を最小化するという発想です。
 |
 |
1.2 単回帰と多重回帰
1.1 差分の二乗和を最小化の図は、切片の高さ![]() の部分を除いて説明変数
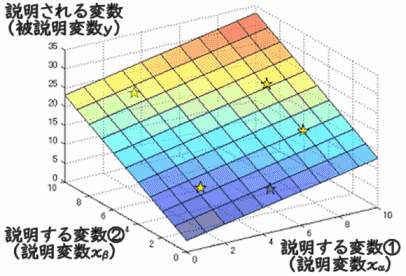
の部分を除いて説明変数![]() が1種類なので単回帰と呼ばれます。一方、下図は2種類の説明変数による回帰分析です。2種類以上の説明変数による回帰分析を多重回帰と言います。単回帰では最小化の対象は星と線の差分の二乗和ですが、多重回帰ではあてはめる線が板になります。それでも二乗和を最小化するという発想自体は同じです。四次元以上になると想像できませんが、イメージは二次元が三次元になる時と同じです。
が1種類なので単回帰と呼ばれます。一方、下図は2種類の説明変数による回帰分析です。2種類以上の説明変数による回帰分析を多重回帰と言います。単回帰では最小化の対象は星と線の差分の二乗和ですが、多重回帰ではあてはめる線が板になります。それでも二乗和を最小化するという発想自体は同じです。四次元以上になると想像できませんが、イメージは二次元が三次元になる時と同じです。
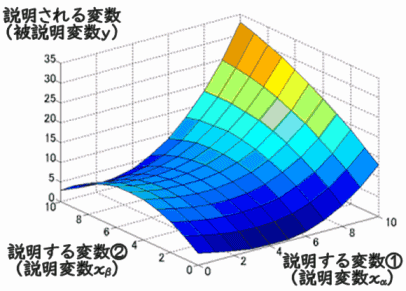
1.3 曲線の回帰線
回帰分析(最小二乗法)によって引かれた線を回帰線と言います。単に最小二乗法という場合、回帰線は直線となり線形と呼ばれます。線形の場合は、1.2 単回帰と多重回帰の図のように![]() が『0→1』に上昇する時と『30→31』に上昇する時とで
が『0→1』に上昇する時と『30→31』に上昇する時とで![]() に与える効果は、同じ
に与える効果は、同じ![]() で等しくなります。ただ、線形の中でもあらかじめlogをとって対数変換をしたり、二乗項
で等しくなります。ただ、線形の中でもあらかじめlogをとって対数変換をしたり、二乗項![]() や交差項
や交差項![]() を説明変数に入れたりすることで、説明変数を元の値に戻すと下図のような曲がった回帰線を描くことができます。
を説明変数に入れたりすることで、説明変数を元の値に戻すと下図のような曲がった回帰線を描くことができます。
目次 : (2)分析ツールでの回帰分析の手順に続きます。