[Excelにおける回帰分析 （5）説明変数に関する出力]

Excel（エクセル）における回帰分析の手順と出力の意味を説明します。
このページでは、説明変数に関する出力を説明します。

目次 ： （4）回帰分析全体に関する出力からの続きです。

このページでは、以下のように表示される説明変数に関する出力を説明します。

5.1　〔推定〕係数：説明変数1単位の増加⇒被説明変数への効果

〔推定〕係数は、説明変数の1単位の増加⇒被説明変数への効果の推定値を示しています。 回帰分析の推定係数は、3.3　推定係数は平均的な効果になるに示したように平均的な効果に対応しています。また、切片は他の説明変数が全て0の時の被説明変数の当てはめ値を示しています。

• 説明変数の単位を変え（万円を円にする等）10000倍にした場合、推定係数は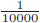倍され、調整されます。

5.2　〔推定係数の〕標準誤差：推定係数の不確かさ

推定係数は、あくまで推定しているわけですから、真の係数からの乖離が予想されます。この乖離の指標が推定係数の標準誤差です。〔推定係数の〕標準誤差は、推定係数の不確かさを示しています。 推定係数の標準誤差が小さいと、推定精度が高いことになります。標準誤差は、以下のような要因によって変化します。

[2]〜[4]に関して、乱数データの[乱数シート]の設定を変えてF9を押すことで確認できます。[2]に関しては、〈F4, F5〉の値を大きくすると説明変数のばらつきを大きくなり、推定係数の標準誤差が減少することが分かります。[3]に関しては、〈B7〉の値を大きくするとエラーのばらつきが大きくなり、推定係数の標準誤差が増加することが分かります。[4]に関しては、〈B6〉の大きさを[-1〜1]の間で変更して、説明変数同士の相関を設定できます。説明変数のとが独立となる0を入力すると、どちらの説明変数の効果かが判別しやすく、標準誤差が小さくなることが分かります。一方で±1に近い値を入力すると、推定係数の標準誤差は大きくなることが分かります。

• 説明変数の単位を変え（万円を円にする等）10000倍にした場合、標準誤差は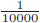倍され、調整されます。
• 説明変数の相関係数が±1で、完全な多重共線性がある場合はどちらの説明変数の効果かを判別できません。Excelの回帰分析では、自動で完全な共線関係にある説明変数を省き、省いた説明変数の標準誤差は0になります。なお、Excelが自動で説明変数を省いた場合、〈分散分析表〉の結果は不正確になります。

5.3　t〔値〕：基準精度で評価した推定係数

推定係数の標準誤差は、推定精度と表裏一体です。よって、標準誤差で調整すれば、基準の推定精度で推定係数を評価できます。以下の(22)式のように、t値は標準誤差で割ることで基準精度で評価した推定係数です。

(22)

推定係数の絶対値が大きければ、t値の絶対値も大きくなります。また、推定係数の標準誤差が小さければ(22)式の分母が小さくなり、t値が大きくなります。

• 説明変数の単位を変え（万円を円にする等）10000倍にした場合、分子の推定係数も分母の標準誤差も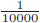倍され、t値は変わりません。

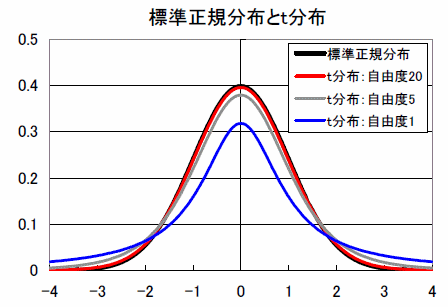
t値を用いて『説明変数の真の効果が0である』という帰無仮説を検定することができます。帰無仮説が正しければ、t値はt分布に従うことが知られています。t分布は、下図のように0を中心に左右対称にばらつく山形の分布です。t分布は自由度が上がると標準正規分布に近づきます。自由度が20以上なら、実務上は標準正規分布と考えて差し支えありません。t分布や標準正規分布において、絶対値2からはみ出す面積の割合は、プラス側とマイナス側のそれぞれ約2.5%で両側約5%です。帰無仮説のもと では約95%の確率で、t値は絶対値2以下に収まります。

• 中心極限定理と擬似正規乱数でF9を押せば、標準正規分布において約95%が±2の範囲に入ることが視覚的に確認できます。

t値が絶対値2以下に収まれば、『前提としていた帰無仮説のもと、約95%の確率の範囲で発生するありふれたt値だった』という解釈になります。 一方で、t値が絶対値で2を超えた時の解釈は、二通りあります。一つの解釈は『帰無仮説のもとで、5%以下でしか発生しない珍しいt値だった』です。もう一つの解釈は『5%以下でしか発生しないt値が出るのは不自然だ。前提とした「説明変数の真の効果が0である」という帰無仮説が間違っていた。』です。どちらの解釈をすべきかは分析者や読者の判断にも依存します。ただt値が約1.7であれば『10%で発生する珍しいt値だった』と言っても苦しくありませんが、t値が約2.5であれば『1%で発生する珍しいt値だった』と言うのは苦しくなります。 t値の絶対値が大きいほど『珍しいこと』という解釈より『不自然なこと⇒前提とした帰無仮説が間違っていた。』という解釈の方がもっともらしくなります。

• 『ありふれたt値』と解釈する範囲に入っても、説明変数の真の効果が0でないケースは十分考えられます。この範囲に入っても『帰無仮説を否定しにくい』と言えるだけで『帰無仮説が正しい』とは言えません。
• 代表的な有意水準や自由度におけるt値は、統計の教科書の巻末などにあるt分布表で照合できます。またExcel関数で[=TINV(確率, 自由度)]を使うこともできます。両側5%、自由度47では[=TINV(0.05, 47)]と入力すると、2.012と出力されます。

キリの良さや慣例から、判定基準を両側で5%（片側で2.5%）とすることが一般的です。 この場合、前述したようにt値が絶対値で2を超えているかを目安にできます。t値が絶対値で2を切っていれば『帰無仮説の前提のもと、約95%の確率の範囲で発生するありふれたt値⇒効果のない説明変数かもしれない。』という解釈になります。一方で、t値が絶対値で2を超えていれば『帰無仮説の前提のもとでは、5%以下でしか発生しないt値⇒効果のある説明変数と考えるのが自然である。』となります。

• 『両側5%の有意水準』といった形で、有意水準(significance level)という用語も使われます。

また、t値を用いた検定は『推定精度をふまえて、効果が0なのか？』を判定しています。このため『推定係数の絶対値が小さくとも、推定精度が高い変数』を効果のある説明変数と判定します。 一方で『推定係数の絶対値が大きくとも、推定精度が低い変数』を効果のない説明変数かもしれないと判定します。t値は、良くも悪くも不確かさを考慮しているので推定係数と使い分ける必要があります。

• 万単位の標本があるデータでは、5.2　〔推定係数の〕標準誤差の[1]から推定係数の標準誤差が極端に小さくなります。この場合、0に近い推定係数であっても、t値は極めて大きくなります。

5.4　P値：t値の検定の境目となる確率

自由度が低い場合や両側5%以外の判定基準を用いる場合など、絶対値2を目安にするt値の判定ができない場合もあります。統計の本にあるt分布表を見れば、各自由度とt値で、帰無仮説を前提とした場合に収まる判定基準を調べることができます。しかし、t分布表は紙面の都合から、区切りの良い自由度や判定基準しか掲載されていません。また、検定のたびに自由度を照合してt分布表を見るのは面倒です。そうした面倒なことは、コンピューターに任せて判定基準の境目を出力するのがP値です。 P値は『説明変数の効果が0である』という帰無仮説のもとで、分析結果のt値が出る境目の確率を示しています。

• p値と小文字で表記される場合もあります。また、P値には有意確率という訳語も使われます。

例えば、自由度が100でt値が2.123の場合、両側5%の判定基準では『帰無仮説のもとで珍しい、もしくは不自然なt値』ですが、両側1%の判定基準では『帰無仮説のもとでも、ありふれたt値』になります。この5%と1%の間に境目があったはずです。ここでt値の右隣のセルにP値が0.0362と表示されることから、境目となる判定基準が両側3.62%であることが分かります。 また、両側5%の判定基準に関しても、『t値が絶対値で2を超えているか？』の目安よりも『P値が0.05を切っているか？』の方が、自由度を考慮していて正確です。

• Excel関数でも[=TDIST(t値, 自由度, 両側=2)]と入力すれば、境目であるP値を表示します。[=TDIST(2.123, 100, 2)]で、0.0362が出力されます。

5.5　〔信頼区間の〕下限, 上限：真の効果がありそうな範囲

推定係数によって一点で示されている値が、真の係数に一致すると考えるのは楽観的ですが、真の係数は推定係数の近くにあると考えるのが自然です。また、推定係数の標準誤差が小さく推定精度が高ければ、推定係数と真の係数はより近いと考えられます。〔信頼区間の〕下限, 上限95%は、信頼係数95%で真の係数がありそうな範囲を示しています。

• ここで確率と言わず、信頼係数という言葉を用いるのは、真の係数は分析者にはっきりと分からないだけで、固有の値があるという発想から来ています。例えば、はっきりと分からなくても『西暦100年に大地震が起こったか？』に対して『確率○%で起こった』とは言いません。しかし、信頼係数という言葉に馴染めなければ、主観的な確率と読みかえてもかまいません。
• 回帰分析のダイアログボックスで95%以外の信頼係数を選択することもできます。また、乱数データの[乱数シート]では、〈R23〉で指定できます。

目次 ： （6）実証分析を行う際の注意点に続きます。