[Excelにおける回帰分析 （2）分析ツールでの回帰分析の手順] 
Excel（エクセル）における回帰分析の手順と出力の意味を説明します。
このページでは、Excelの分析ツールを使った回帰分析の手順を紹介します。
Excelにおける回帰分析（最小二乗法）用乱数データ：乱数を用いて、推定値の挙動を見ることのできるExcel（約100KB）です。
分散の不偏推定量：偏差平方和を（n-1）で割ると分散の不偏推定量になることが視覚的に確認できるExcel（約80KB）です。
中心極限定理と擬似正規乱数：一様分布の標本平均が正規分布に近づくことや統計における検定のアイディアが視覚的に確認できるExcel（約60KB）です。
学校は人的資本を形成するのか? (1)教育の経済学：分布やシミュレーションを使って、学歴と平均賃金の関係を説明するHTMLです。
学校は人的資本を形成するのか? (2)賃金格差の実証分析：日本の学歴間賃金格差の実証分析を説明するHTMLです。
目次 ： （1）最小二乗法の発想からの続きです。
2.1 アドインから分析ツールを追加する
Excelでの回帰分析は分析ツールを使います。これまで分析ツールを使ったことのない場合は、分析ツールをアドインする必要があります。Microsoft OfficeやExcelのCDが必要になる場合があります。
Excel 2003以前の場合
Excelのメニューにある[ツール]⇒[アドイン]をクリックします。表示された候補の中の[分析ツール]にチェックを入れて[OK]をクリックします。
 |
 |
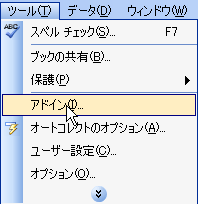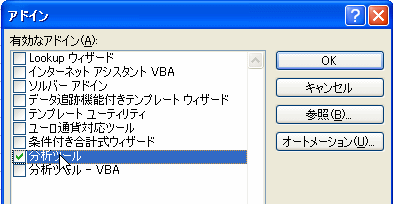Excel 2007の場合
Excel 2007の画面左上の[Microsoft Officeのボタン]をクリックして、表示されたメニューの中から[Excelのオプション]をクリックします。
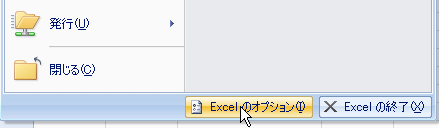
Excelのオプションの中から[アドイン]を選択し、[設定]をクリックします。表示された候補の中の[分析ツール]にチェックを入れて[OK]をクリックします。
 |
 |
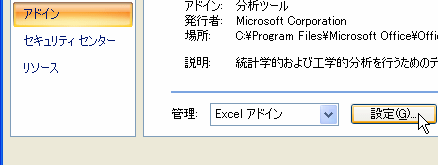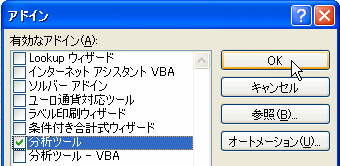2.2 回帰分析用データを縦に並べる
Excelで回帰分析を行うためには、被説明変数
と説明変数
のデータを縦に並べる必要があります。 ここでは例示として、Excelでの回帰分析（最小二乗法）用乱数データを用います。この乱数データでは、被説明変数に対して
と
の2つの説明変数で回帰分析を行います。1枚目の[乱数シート]では、との関係である係数やノイズであるエラーの値を設定することができます。再計算のF9を押すことで、乱数からエラーが再生成されます。[乱数シート]の中には、分析ツールの回帰分析風の出力があり、推定値の挙動を見ることができます。また、変化する[乱数シート]を値で貼り付けて固定したものが[固定シート]です。以降のページでは、回帰分析結果の例として[固定シート]を用いて説明します。
![[固定シート]の値](ols2_fixed.gif)
2.3 分析ツールから回帰分析を実行する
縦に並べたデータを使って回帰分析を実行します。
Excel 2003以前の場合
[ツール]⇒[分析ツール]をクリックします。
Excel 2007の場合
[データ]のタブの中にある[データ分析]をクリックします。
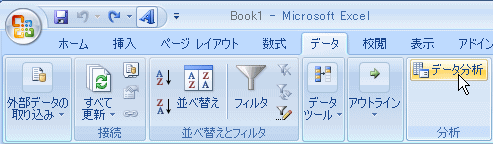
データ分析のダイアログボックスから、[回帰分析]を選択して[OK]をクリックしてください。
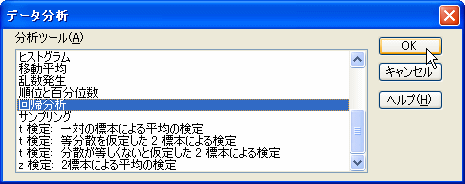
表示された回帰分析のダイアログボックスには、入力Y範囲に被説明変数の1列を、入力X範囲に説明変数の列を指定してください。
のボタンを押せば、マウスで範囲を指定することができます。Excelでの回帰分析（最小二乗法）用乱数データでは、一行目に変数名を入れて、入力Y範囲を〈$B\$10:$B$60〉、入力X範囲を〈$C$10:$D$60〉、出力先を〈$K$10〉に指定しています。回帰分析の指定が終われば、[OK]をクリックします。
- Excelの回帰分析において、説明変数に指定できるのは最大16種類です。
- 推定結果に変数名を表示する場合は[ラベル]にチェックを入れて、変数名を入力範囲の第一行目に指定してください。
- 入力範囲の$はExcelで絶対参照を示す記号です。マウスでセルを指定した場合は、自動的に$が付きます。打ち込む場合は、$不要で『左上セル:右下セル』と記入できます。
- 出力オプションに〈$K$10〉のようにセルを指定すれば、同じシートの指定したセルから右下に回帰分析結果が出力されます。新規ワークシートにすれば他のシートに出力します。
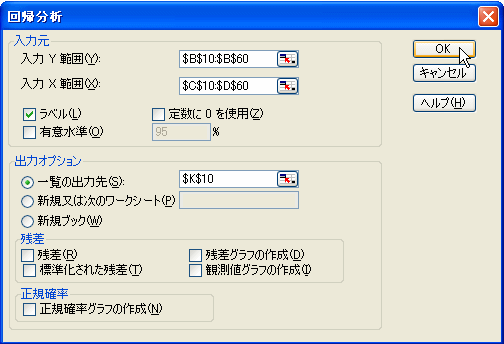
指定した出力先には、下の画像のような回帰分析の結果が表示されます。
目次 ： （3）最小二乗法の性質に続きます。