[Do Schools Form Human Capital? (1)Economics of Education]
This page outlines "A fallacy of wage differentials: wage ratio in distribution".
I show a misleading point of the wage ratio with a simple example.
This page is continued on Do Schools Form Human Capital? (2)Wage Differentials in Japan.
(1)Economics of Education and (2)Wage Differentials in Japan are also written in Japanese.
Do schools form human capital? Distributional divide and cohort-based analysis in Japan is full text PDF (700KB) analyzes wage gap of Japan
Learn fallacy of wage differentials with cohort data in 10 minutes is PDF (140KB) of this Web page for print. It's 6-page summary of the above two papers
Simulation of Ratio between Averages is Excel (50 KB) simulation of the ratio between average or wage ratio with an arbitrary distribution and effect of education.
1. Economic Theories about Education
Across the world, education is perceived to be connected with getting a job and earning wages. Economics has two major theories about education. One is human capital theory, and the other one is signaling theory. The following table shows the role of higher education in each theory.
| theory | the role of higher education |
| human capital theory | Education increases an individual's productivity and wages. |
| signaling theory | Individuals can exhibit their productivity and diligence by entering and graduating from educational institutions. (The signaling theory doesn't require increase of productivity.) |
Even if the data on wages and educational status are available, it is difficult to distinguish between the in-school effects from the pre-school productivities. Moreover, one theory does not violate the other. Previous attempts to determine which theory is more practical have been inconclusive. When you finish reading (2)Wage Differentials in Japan, you see the conclusion in the case of Japan.
- Because human capital has been considered as a source of economic growth as well as physical capital, intelligence and skill were named human capital in macroeconomics.
- The signaling theory is also called screening theory. Job applicants or students send signals of educational status to exhibit their productivities. Employers or firms screen students by receiving the signals. The theory has two names from different viewpoints.
- Prof. Becker, who is authority on human capital theory, received Nobel Prize in economics in 1992. Prof. Spence, who is authority on signaling theory, received Nobel Prize in economics in 2001. (Bank of Sweden Prize in Economic Sciences in Memory of Alfred Nobel)
2.1 The Wage Ratio as Wage Differential
Apart from the economic theories about education, wage differentials have been a topic of debate in media and policymaking. A wage ratio is a basic index of the wage differential across educational statuses. The wage ratio is calculated by dividing the average wage of people with higher educational status by the average wages of those having lower educational status. In most cases, the higher educational status means college graduates, while the lower one means high-school graduates. In other words, the primary wage ratio is represented as follows.
the wage ratio between college and high-school graduates =![]()
The wage ratio is easy to interpret 1.2 as 20% higher or 1.2 times. Rise in prices has no effect on the wage ratio. However, the wage ratios
are misleading indexes of wage differentials. This is the introductory
part of the analyses.
- The wage ratio is used for trend analyses (e.g. Concise Encyclopedia of Economics: Human Capital, Current Population Reports: July 2002) and international comparisons (e.g. OECD Science, Technology and Industry Scoreboard 2007).
- Academic papers often take the logarithm of the wage ratio. Monotonic transformation does not change the essence.
2.2 A Misleading Point of the Wage Ratio
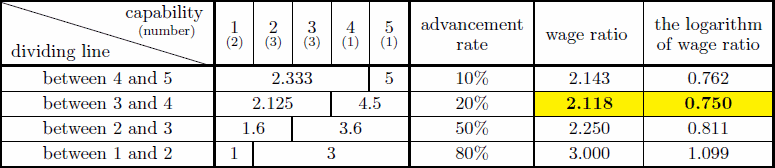
Let me present the misleading point of the wage ratio with a simple example. Three men whose productivities are A > B > C, respectively come into the world. A is twice as productive as B, and A is three times as productive as C. Three men earn $300, $200, and $100 respectively according to each productivity. An individual goes to higher education in order of their potential productivities. I tentatively assume that education has no effects on productivity and wage.
In the past, only A went to higher education. Nowadays, both A and B go to higher education. How does the wage ratio change?
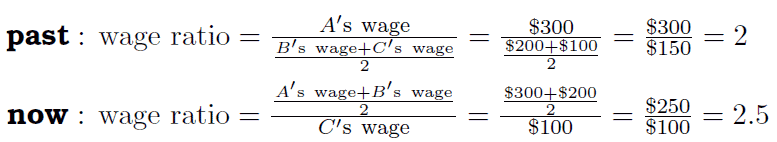
As a matter of course, wage of each individual remain constant because education has no effect. However, the wage ratio does increase from 2 to 2.5.
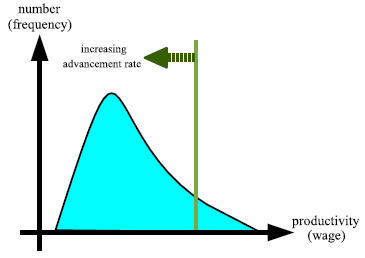 The example of {$100, $200, $300} is a simplified version of a uniform distribution that is high, middle, and low levels of productivity exist evenly. The increasing advancement rate necessarily increases the wage ratio in any uniform distribution. Meanwhile, it is natural to assume that the actual wage and productivity follow a mountain-shaped distribution as shown in the right figure.
The example of {$100, $200, $300} is a simplified version of a uniform distribution that is high, middle, and low levels of productivity exist evenly. The increasing advancement rate necessarily increases the wage ratio in any uniform distribution. Meanwhile, it is natural to assume that the actual wage and productivity follow a mountain-shaped distribution as shown in the right figure.
In most mountain-shaped distributions, the wage ratio increases after an initial decline with an increase in the advancement rate. The following table shows a relationship between the advancement rate and the wage ratio that can be examined by hand calculation.
The minimum wage ratio cell is colored with yellow. In this numerical value, the minimum advancement rate (10%) brings the wage ratio to 2.143. The second-minimum advancement rate (20%) brings the minimum wage ratio to 2.118. The advancement rate of more than 50% increases the wage ratio. In summary, the wage ratio begins to increase reversely after a decline if the advancement rate increases. The wage ratio changes even if there are neither individual wage variations nor the effects of education.
For the sake of simplicity, the above examples have assumed that education has no effect on wage. Even if I assume that education has effects on wage, the main result is very similar to those in the case of no effect. If you would like to simulate ratio between averages with an arbitrary distribution and effect of education, use Excel simulation of Simulation of Ratio between Averages.
We have hitherto assumed that people go to higher education strictly in the order of their potential productivity. However, the decision to pursue higher education depends not only on productivity or test scores but also on other factors like household income, location, character. Moreover, some people earn poor scores but earn a fortune and vice versa. The realistic assumption is that there is a positive correlation between the propensity to go for higher education and the potential wages of such people. Even though a one-to-one correspondence between educational status and wage is not satisfied, the one-to-one correspondence can substitute for a positive correlation with regard to average wage.
The lower-left movie indicates a two-dimensional distribution of academic ability and wage. A dividing board on the academic ability side visually partitions the two-dimensional distribution. If the partitioned distributions are seen from the wage side, they are wage distributions by educational status. The lower-right movie demonstrates the transitions of wage distributions by educational status with increasing advancement rate. The red solid line shows the wage distribution of higher educational status. The blue dashed line shows the wage distribution of lower educational status. Wage distributions across educational status overlap realistically in the correlation setting. Meanwhile, the average wages by educational status are the same as that in the case of one-dimensional distribution. If there is a positive correlation between academic ability and wage, the wage ratio of averages is the same as that in the case of one-to-one correspondence.
2.3 Key Points of Wage Ratio
The key points in the examples and simulations are as follows:
The advancement rate to higher education has been increasing in most countries. The changes in the wage ratio are natural outcomes in any case as indicated by [1]. Thus, the wage ratios are misleading indexes of wage differentials.
(2)Wage Differentials in Japan presents empirical wage analyses of Japan on the basis of this page.