[学校は人的資本を形成するのか? (2)賃金格差の実証分析]

学校は人的資本を形成するのか？ 〜分布区分とコーホート分析〜 ［実証:日本のみ］を簡潔に説明します。
このページでは日本の賃金データを使って、高等教育の人的資本形成（⇒生産性上昇）効果を検証します。
教育に関する経済理論、賃金倍率の問題点に関しては、前ページの(1)教育の経済学を読んでください。

If you prefer English, go to (1)Economics of Education and (2)Wage Differentials in Japan.

教育に関する経済理論や賃金格差の測り方の問題点を示した学校は人的資本を形成するのか? (1)教育の経済学からの続きです。

3.1　大卒・高卒間の賃金倍率

賃金格差の測り方の問題点が実際、どの程度の影響を持っているかをデータを使って示します。使用するデータは厚生労働省によって調査・公表されている賃金構造基本統計調査です。 年収換算の指標である（6月における）きまって支給する現金給与額×12+[年間賞与その他特別給与額]を分析用の賃金データとして用います。

• 賃金構造基本統計調査は賃金センサスとも呼ばれ、世界最大規模の賃金調査です。2003年の調査結果は7万の事業所、151万人の労働者のデータから作られています。
• 賃金構造基本統計調査は、民営の事業所の賃金を主な統計の対象としています。この分析用のデータも民営の事業所のみの統計から作成しています。
• この年収換算した賃金は、労働経済学の学術論文でもよく用いられます。また、時給換算の賃金を用いても、このWebページの基本的な結論は変わりません。

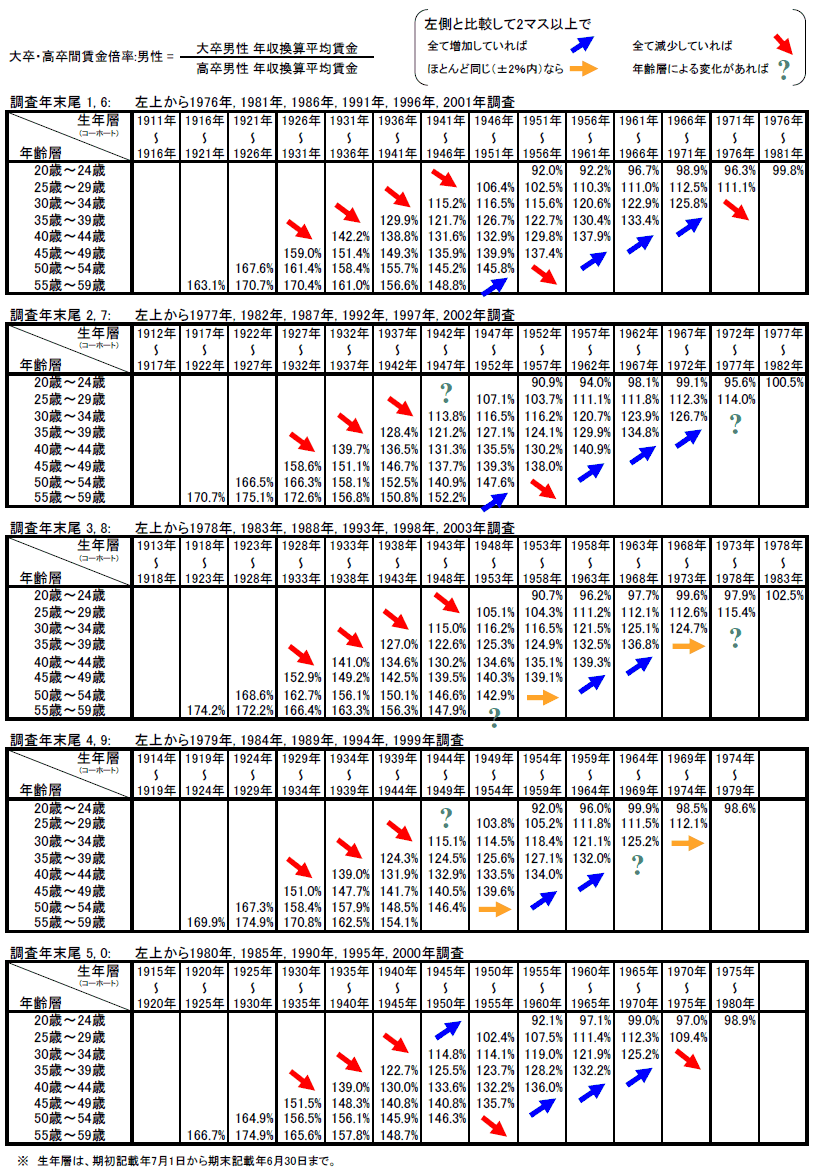
まず、政府資料や労働経済学の論文で扱われることの多い男性労働者の大卒・高卒間の賃金倍率を示したものが下の5つの表です。賃金構造基本統計調査は5歳区分でデータが記載されています。1つの表の中に5年おきの調査結果を並べることで、5年前の調査からちょうど5歳年をとった移り変わりを見ることができます。横のラインの年齢層に対応して縦のラインを生年層と呼び、俗に言う世代を指しています。表の中の左隣の列は5歳年上の生年層(世代)を意味します。左隣の生年層と賃金倍率を比較して、増減を矢印で記入しています。

表の中の矢印は、世代の移り変わりに伴い賃金倍率が縮小後に拡大していることを示しています。その中で1950年代と1970年代の生年層には、不規則な変動があります。就職時点におけるオイルショックやバブル崩壊の賃金への影響が長期的に残ることを示しています。

• 同じ属性の一団を統計学ではコーホート（cohort）と呼びます。表中でのコーホートは、同じ期間（＝生年層）に生まれた一団を指します。
• 賃金構造基本統計調査における大卒は、大学院卒を含みます。
• 就職時点の景気の影響が数十年経っても残るという点は、日本の賃金格差に関する他の学術論文と整合的です。
• 上記の賃金倍率の表は、生涯賃金や進学の収益率（内部収益率、ミンサー型賃金関数）の算出や推定に関する注意点を明示します。平成17年版の国民生活白書、平成19年度の経済財政白書、Education at a Glance 2007 をはじめ、ほとんどの進学と賃金に関する分析は、一時点の賃金データをもとに算出しています。こうした算出方法では、上の表内で各調査年に対応する斜めのラインの賃金格差を用いていることになります。実際の賃金格差は、表内の縦のラインである生年層から大きな影響を受けており、斜めのラインである各調査年はどの生年層にも対応していません。このため、各調査年のデータから得られた収益率の水準や変化を論じても無意味です。また、後述するように表内の縦のラインに現れる変化に関しても、そのほとんどは分布区分の見せかけによるものです。

大まかには、生年層が右に行くと大学進学率が上昇しているので、表にある変化は2.3　賃金倍率の要点まとめの[2]と一致しています。しかし、数値例や平均間倍率の簡易シミュレーションが実証分析と一致しない点もあります。それはシミュレーションが大卒と高卒の2種類に分けたのに対して、賃金構造基本統計調査には4種類の学歴区分が存在する点です。賃金構造基本統計調査における学歴は、[高卒]と[大卒]に加えて[専門学校・短大卒]と[中卒]という区分があります。注目されやすい大卒・高卒間の賃金倍率でも、上の表の矢印に表れるきれいな変化がありますが、[専門学校・短大卒]と[中卒]を加えてシミュレーションと整合的に扱いたいと思います。

3.2　分位数間倍率で高等教育の効果を検証

4つの学歴区分をシミュレーションと整合的扱うと言っても、分布の形をきちんと決めずに4分類のままで分析することは困難です。また、分布の形を決めようにも、山形以上に生産性（賃金）の値まで決められる明確な根拠はありません。簡単な解決策は、以下のように4つの学歴区分を労働者数の加重平均によって2つにまとめてから分析することです。

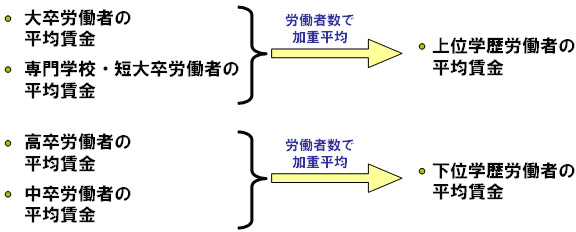
しかし、こうした労働者数による加重平均が正当化されるためには前提条件が必要です。その前提条件は、高等教育の賃金への効果が無視できるほど小さいことです。もし、この効果が大きければ、上位と下位の各学歴内での学歴シェアが加重平均賃金に影響を与えてしまい、労働者数のみで加重平均をとることはできません。加重平均の前に、高等教育の効果が無視できるほど小さいかを調べる必要があります。

各学歴の平均賃金を用いた指標から高等教育の効果を測ることは困難ですが、各学歴の平均賃金を使わずに高等教育が賃金に与える効果を調べる方法があります。2.2　賃金倍率の問題点と同じく、生産性の高い人（Aさん）、普通の人（Bさん）、生産性の低い人（Cさん）の例を使って説明します。 賃金倍率の問題点で示したように高等教育が賃金に効果を与えても、与えなくても一般に

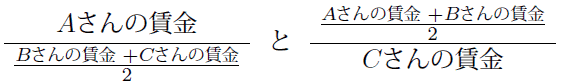
は一致しません。このため、学歴別の平均賃金による指標を用いて高等教育の効果を計測することは困難です。もし、効果があれば一致せず、効果がなければ一致する指標があれば、高等教育の効果を計測することができます。Aさん、Bさん、Cさんの例で使える指標は、単純に

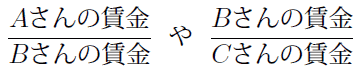
です。3人中1人しか大学に行かなかった時代から3人中2人大学に行く時代になって、Aさんに加えてBさんまで大学に行くようになったとします。もし大学が賃金にプラスの効果を持てば、分母の増加からAさんの賃金/Bさんの賃金は縮小し、分子の増加からBさんの賃金/Cさんの賃金は拡大します。学歴で分けずに世代内全体での上位25％、中央値（50％）、下位25％の分位数を使えば、分布を決めずとも高等教育が賃金に与える効果を調べることができます。

3.1　大卒・高卒間の賃金倍率の表と同じ形式で男性労働者の分位数間倍率を整頓し、計量経済学の手法を用いて年齢層と生年層の効果に分解します。分解して得られた下位25％と中央値間の生年層効果を描いたのが左下グラフ、中央値と上位25％間の生年層効果を描いたのが右下グラフです。グラフの中の点線は、労働者の学歴割合の分かれ目を示しています。中央値 in 高卒は、その生年層より左（前）では中央値の労働者は中卒でしたが、その生年層より右（後）では高卒になったことを示しています。上位分位数の学歴が変化した場合は点線の上側に、下位分位数の学歴が変化した場合は点線の下側に説明を付けています。

• 計量経済学における固定効果モデルを使って切片、年齢層効果、生年層効果に分解しています。固定効果モデルのアイディアは、Excelにおける回帰分析（ダミー変数）を参照してください。

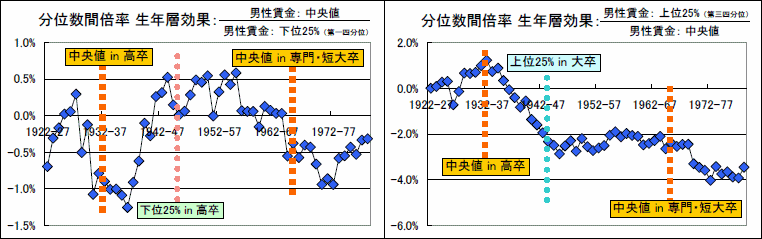
グラフを大まかに見ると、上位分位数の学歴が変化した際に倍率は下がり、下位分位数の学歴が変化した際に倍率が上がっています。これは高等教育に進学することで賃金に対して差し引きでマイナスの効果があることを示唆しています。進学しない人の大半は、進学する人より早めに働き始めます。職場でも学んだり、技能を身につけたりすれば生産性（賃金）は上昇します。もし、高等教育と職場訓練で賃金に及ぼす効果が等しければ差し引きゼロとなって、学歴割合は分位数間倍率に影響を与えません。実証結果は、高等教育の効果は職場訓練の効果を下回っており、進学することで差し引きマイナスの効果があることを示唆しています。

• 各分位の学歴が変わる少し前の生年層で分位数間倍率が変化しているようにも見えます。高等教育が差し引きでマイナスの効果を持つ場合は、前倒しで変化する可能性があります。

しかしながら、公表されているデータから高等教育が賃金に与える効果を正確に測ることは困難です。1960年代以降の生年層では、学歴割合の変化に関係なく分位数間の倍率が縮小する傾向にあります。こうした変動を含め、高等教育の効果と無関係な要因から分位数間倍率が変動している可能性はあります。また、数十％の変化がある平均間の倍率の変動に比べ、分位数間倍率の変動は数％しかありません。分位数間倍率の変化の全てを高等教育の効果と見なしても、その絶対値は最大で数％です。ただ、高等教育の効果は職場訓練との差し引きでゼロに近い値であるとは言えます。その効果が十分ゼロに近ければ、労働者数の加重平均による賃金倍率の導出が近似計算として正当化されます。

3.3　加重平均での賃金倍率

4つの学歴区分を労働者数の加重平均によって2つにまとめて、賃金倍率を計算します。 [中卒]と[高卒]を下位学歴とし、[専門学校・短大卒]と[大卒]を上位学歴とした賃金倍率から、生年層の効果を抽出してグラフに表します。比較のために3.1 大卒・高卒間の賃金倍率の表で示した大卒・高卒間の賃金倍率を用いたのが左下のグラフ、労働者数の加重平均から算出された上位学歴・下位学歴間の賃金倍率を用いたのが右下のグラフです。

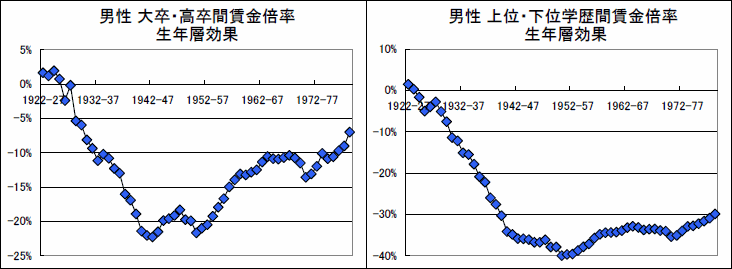
右のグラフは平均間倍率の簡易シミュレーションと同じく、2種類の学歴による賃金倍率の変化となっています。シミュレーションの結果と同様、進学率の上昇によっていったん縮小して拡大する変化を示しています。また、右のグラフでは加重平均をとることで短大と大学といった形で就職時点がばらつくので、左のグラフより不規則な変動は薄まっています

• 女性労働者に関しても高等教育の効果は差し引きマイナスであること、加重平均による賃金倍率は滑らかな縮小拡大の変化を示すことは、男性労働者と共通しています。また、賃金倍率の測り方の問題は、学歴別の男女間賃金格差にも影響を与えます。

さらには実証分析の統計量によると、生年層と年齢層の効果で賃金倍率全体の変動の99％以上を説明できます。特定の時期に学歴間賃金格差が大きく変化したことはなく、1990年代のコンピューターの普及も賃金格差にあまり影響がなかったようです。学歴間賃金格差の変化のほとんどは、分布区分の見せかけによるものです。

• 学歴間の賃金格差が特定に時期に変化していないことは3.1　大卒・高卒間の賃金倍率の表からも確認できます。もし特定の時期に学歴間の賃金格差が変化したなら、大卒・高卒間賃金倍率の表には縦の生年層の効果でも横の年齢層の効果でもなく、斜めの調査年の効果として現れるはずです。斜めの効果が小さいために、縦の生年層の効果は表中の矢印に現れる縮小拡大を示します。

3.4　実証分析の要点まとめ

実証分析の要点を列挙すると

となります。

4. 終わりに

1.　高等教育に関する経済理論に人的資本論とシグナリング理論の論争を示しましたが、3.4　実証分析の要点まとめの[3]に示したように、少なくとも日本ではシグナリング理論が現実的です。一般論として、高等教育は労働者育成を得意としていません。潜在的に2の生産性を持つ人は『自分の生産性が1ではない』ことを示すために進学して、お金と時間をかけて仕事に生かせる生産性を1.9に下げている状況かもしれません。個々人としては合理的な行動であっても、社会としては技能形成や経済成長に損失を被っている可能性があります。

古代から学習や教育は美徳とされ、文化的な側面も持ちます。しかし、これで良いのかをきちんと考え、話し合う必要があります。