[Excelにおける回帰分析 (6)実証分析を行う際の注意点] 
Excel(エクセル)における回帰分析の手順と出力の意味を説明します。
このページでは、実証分析を行う際の注意点を示します。
Excelにおける回帰分析(最小二乗法)用乱数データ:乱数を用いて、推定値の挙動を見ることのできるExcel(約100KB)です。
分散の不偏推定量:偏差平方和を(n-1)で割ると分散の不偏推定量になることが視覚的に確認できるExcel(約80KB)です。
中心極限定理と擬似正規乱数:一様分布の標本平均が正規分布に近づくことや統計における検定のアイディアが視覚的に確認できるExcel(約60KB)です。
学校は人的資本を形成するのか? (1)教育の経済学:分布やシミュレーションを使って、学歴と平均賃金の関係を説明するHTMLです。
学校は人的資本を形成するのか? (2)賃金格差の実証分析:日本の学歴間賃金格差の実証分析を説明するHTMLです。
目次 : (5)説明変数に関する出力からの続きです。
基準となる回帰分析の例
このページでは、実証分析を行う際の注意点を説明します。例として、被説明変数を傘屋での【傘の販売本数】、説明変数を【降水量、風速、傘の価格】とした以下の(23)式を用います。[1]、[2]、[3]は水色の部分の回帰分析の式、[4]は黄色の部分のエラー、[5]と[6]はデータに関する注意点です。
| (23) |
6.1 回帰分析の式の形
(23)式の形では【降水量】が『0mm→1mm』でも『100mm→101mm』でも一定の効果が【傘の販売本数】にあることを前提にしています。また、【降水量】と【風速】は独立して【傘の販売本数】に影響を与える形になっており、雨と風の相乗効果は考えていません。(23)式の形では、説明変数の効果が水準に依存せず一定であること、説明変数同士の相乗効果がないことをあらかじめ決めつけています。一般的に、あらかじめ決めつけた式の形が複雑な現実の関係を正しく表していると考える方が不自然です。実証分析において、回帰分析の式の形(関数形)はどうやっても近似にすぎませんが、無理のない近似になっている必要があります。『回帰分析の式の形は、現実の関係の無理のない近似になっているか?』という注意点があります。
- 式の形を決めつけないノンパラメトリック回帰もありますが、推定結果の表示や解釈が難しくなります。
- 式の形は標本の範囲を含めて考えます。日常的な【降水量】のみの範囲では、水準に依存せず一定の効果と近似しても無理がないかもしれません。しかし、その回帰分析での推定係数は、大雨において【降水量】が【傘の販売本数】に与える効果とは異なると考えられます。
[変数の変換]
式の形が現実の良い近似となるように、被説明変数や説明変数をあらかじめ変換しておく場合があります。例えば、被説明変数![]() に自然対数をとることで推定係数
に自然対数をとることで推定係数![]() は
は![]() が1増えた場合の
が1増えた場合の![]() の変化率として解釈できます。 また、説明変数
の変化率として解釈できます。 また、説明変数![]() に自然対数をとることで推定係数
に自然対数をとることで推定係数![]() は
は![]() が1%増加した場合の
が1%増加した場合の![]() への効果と解釈できます。 (23)式の
への効果と解釈できます。 (23)式の![]() の解釈は、『傘の価格が1円上昇した時の傘の販売本数に与える効果』ですが、以下の(24)式の
の解釈は、『傘の価格が1円上昇した時の傘の販売本数に与える効果』ですが、以下の(24)式の![]() は『傘の価格が1%上昇した時の傘の販売本数に与える効果』と解釈できます。
は『傘の価格が1%上昇した時の傘の販売本数に与える効果』と解釈できます。
| (24) |
- 自然対数の微分が
 と分数になることから、被説明変数
と分数になることから、被説明変数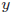 に対数をとった場合は
に対数をとった場合は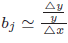 となります。
となります。
- 自然対数のExcel関数はnatural logarithmのln(数値)です。Excel関数でlog(数値)として対数の底を省略すると、10を底とする常用対数になるので注意してください。
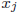 と
と の双方に自然対数をとれば、推定係数は変化率と変化率の比である弾力性として解釈できます。
の双方に自然対数をとれば、推定係数は変化率と変化率の比である弾力性として解釈できます。
[ダミー変数]
標本として使うデータの中に地域、時点などのグループがあれば、ダミー変数を用いてグループの違いを回帰分析に入れることができます。グループAとグループBで切片が異なる可能性のある場合は、以下の(25)式のように定数項ダミーを説明変数に加えます。
| (25) |
定数項ダミーは基準のグループAなら0、グループBなら1を入力した列です。Excelの回帰分析にこの列を説明変数として加えることで、定数項ダミーを加えた回帰分析となります。
(25)式においてグループAの切片の推定値は![]() ですが、グループBの切片の推定値は
ですが、グループBの切片の推定値は![]() となります。
となります。
また、グループによって説明変数の効果が異なる可能性を考え、以下の(26)式のように係数ダミーを設定することもできます。
| (26) |
(26)式の係数ダミーは(25)の定数項ダミーと同じ値が入り、【降水量】の推定係数は基準のグループAには![]() 、グループBには
、グループBには![]() となります。しかし、(26)式の形では、Excelで回帰分析を実行できません。Excelで回帰分析が実行できるようにするには、以下の(27)式のように【降水量】をグループ毎に分け、該当グループ以外を0とした新しい説明変数の列を作ります。
となります。しかし、(26)式の形では、Excelで回帰分析を実行できません。Excelで回帰分析が実行できるようにするには、以下の(27)式のように【降水量】をグループ毎に分け、該当グループ以外を0とした新しい説明変数の列を作ります。
| (27) |
(27)式において、【降水量】の推定係数はグループAには![]() 、グループBには
、グループBには![]() となります。
となります。![]() と変換すると、(26)式と(27)式の回帰分析の結果は同じになります。
と変換すると、(26)式と(27)式の回帰分析の結果は同じになります。
グループA、グループB、グループC、・・・と3グループ以上ある場合にも同様の手順で定数項ダミー、係数ダミーを指定ができます。 また、地域と時点といった形で複数の種類のグループに別々のダミー変数を設定することもできます。
- 地域と時点といった形で複数の種類のグループを設定すると、パネルデータに対する固定効果モデルになります。学校は人的資本を形成するのか?の賃金格差の実証分析では、年齢層と生年層での固定効果モデルから賃金格差の変化をグラフに表しています。
[近似の確認と方法]
多重回帰であっても、![]() 種類目の説明変数
種類目の説明変数![]() と被説明変数
と被説明変数![]() の散布図を見ることで、両者の関係に見当をつけることができます。また、候補の式の形で回帰分析を行い、得られた当てはめ値
の散布図を見ることで、両者の関係に見当をつけることができます。また、候補の式の形で回帰分析を行い、得られた当てはめ値![]() と推定エラー
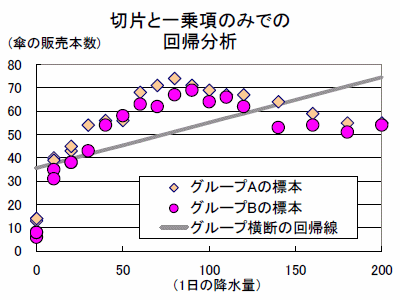
と推定エラー![]() の散布図を用いて確認できます。例えば、下の図では切片と一乗項だけの式では良い近似とはならないことが分かります。また、結果的に得られた
の散布図を用いて確認できます。例えば、下の図では切片と一乗項だけの式では良い近似とはならないことが分かります。また、結果的に得られた![]() と
と![]() の散布図を描けば、
の散布図を描けば、![]() の大きさによって
の大きさによって![]() が偏っていることが分かります。
が偏っていることが分かります。
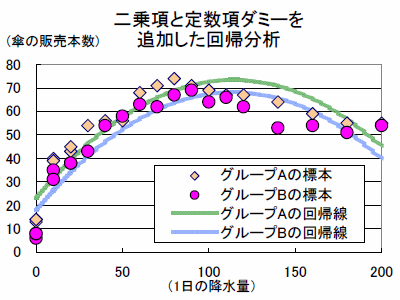
近似の度合いを高める簡単な方法は、![]() の二乗項や
の二乗項や![]() の交差項を説明変数に追加することです。下の図では、上の図に
の交差項を説明変数に追加することです。下の図では、上の図に![]() の二乗項と定数項ダミーを追加することで下の図より現実の関係に近くなっています。しかし、複雑な関係も許容する式の形が望ましい反面、単純化して分かりやすく表すことも重要なのでバランスをとる必要があります。
の二乗項と定数項ダミーを追加することで下の図より現実の関係に近くなっています。しかし、複雑な関係も許容する式の形が望ましい反面、単純化して分かりやすく表すことも重要なのでバランスをとる必要があります。
6.2 必要な説明変数
複数の説明変数を用いる多重回帰では、他の説明変数の効果を調整した上での各説明変数の効果を推定しています。(23)式は【降水量、風速、傘の価格】を用いた多重回帰ですが、感覚的に一番効果が大きそうな説明変数は【降水量】です。しかし、(23)式における【降水量】のデータがなかったり、説明変数であることに気がつかない場合があります。また、雨が降る時には風が強いことが多く、(23)式から【降水量】を抜いて回帰分析を行うと【風速】が大きな効果を持っているという推定結果が得られそうです。しかし、仮に『風が強いだけの日』があっても【傘の販売本数】は伸びそうにありません。必要な説明変数を省くと、他の説明変数の推定値にも悪影響があります。『必要な説明変数が全て回帰分析の式に入っているか?』という注意点があります。
- 【降水量】のデータがないので【湿度】を説明変数に用いるなど、代理変数を使う場合があります。しかし、代理変数の推定値の解釈には注意が必要です。また、6.6 データの正確さの問題も生じます。
この注意点に対しては、必要な説明変数をよく考える必要があります。また、説明変数を入れるか省くかを迷ったら、入れる方が無難です。 一般的に関係のある説明変数を省くと、他の説明変数の推定係数に悪影響があります。一方、無関係の説明変数を入れると推定精度は落ちますが、現実に対応しない推定係数になる傾向はありません。
- 効果や他の推定値への影響がないことを確認してから説明変数を減らしたり、複数の推定結果を示して安定性を論じたりすることがあります。
6.3 効果の方向
(23)式では【降水量、風速、傘の価格】が【傘の販売本数】に与える効果を調べています。しかし、『傘がよく売れる時期や場所では、傘屋が傘の値上げをして利益を出す』という逆方向の効果があるかもしれません。傘の価格は安い方がよく売れるなら(23)式の![]() はマイナスになるはずですが、逆方向の効果があれば
はマイナスになるはずですが、逆方向の効果があれば![]() は0に近づき、プラスになることも考えられます。また、逆方向の効果の極端な例として【降水量】を被説明変数にして【傘の販売本数】を説明変数にすることが考えられます。理屈の上では【傘の販売本数】が伸びても、雨は降らないことが分かります。しかし、機械的な回帰分析では『傘が売れれば、雨が降る』という結果になります。これらの結果を単純に解釈すると『傘を多く売るために値上げをしよう』や『雨を降らせるために傘を買おう』という話になりかねません。『説明変数⇒被説明変数の効果の方向は正しいか?』という注意点があります。
は0に近づき、プラスになることも考えられます。また、逆方向の効果の極端な例として【降水量】を被説明変数にして【傘の販売本数】を説明変数にすることが考えられます。理屈の上では【傘の販売本数】が伸びても、雨は降らないことが分かります。しかし、機械的な回帰分析では『傘が売れれば、雨が降る』という結果になります。これらの結果を単純に解釈すると『傘を多く売るために値上げをしよう』や『雨を降らせるために傘を買おう』という話になりかねません。『説明変数⇒被説明変数の効果の方向は正しいか?』という注意点があります。
この注意点に対しては、効果の方向や経路をよく考える必要があります。また、【降水量、風速】は、『傘屋にはどうにもならないもの』です。こうした説明変数なら『逆方向の効果があるかもしれない』という問題はありません。 しかし、理系の実験と違い、経済などのデータは『景気と失業の関係』『企業の業績と広告費の関係』のように因果が分からないこと、両方向が考えられるケースが多々あります。こうしたケースでは、時間的な前後関係を利用することで『雨が降ってから、傘が売れる』のか『傘が売れてから、雨が降る』のかを識別する場合があります。この場合は、過去の説明変数が将来の被説明変数に影響を与えるという枠組みで回帰分析を行います。また、操作変数法によって対処できる場合もあるので、関心のある方は計量経済学の本を参照してください。
- 逆方向の効果が考えられない対象を取り出すことで、擬似的な実験環境を分析することもあります。
- 『雨が降りそうだから、傘を買う』や『景気の見通しが暗いから、失業が増える』といった形で、時間的な前後関係が効果の方向に対応しない場合もあります。
- 操作変数法の一つである二段階最小二乗法は、推定係数を導出するだけならExcelの分析ツールでも実行できます。
6.4 エラーの形状と分散
Excelの回帰分析の結果は、推定エラー![]() の背後にある真のエラー
の背後にある真のエラー![]() は、以下の(28)式の平均0、分散
は、以下の(28)式の平均0、分散![]() の正規分布から発生することを仮定して導出しています。
の正規分布から発生することを仮定して導出しています。
| (28) |
- (19)式のエラーの標準誤差は
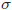 (シグマ)の推定値です。また、(19)式の推定には正規分布の仮定は不要です。
(シグマ)の推定値です。また、(19)式の推定には正規分布の仮定は不要です。
- 中心極限定理の一つとして『同じ分布に従っていなくても、独立な確率変数の和は正規分布に近づく』があります。このため、特に理由がない限り種々のノイズの合計値である回帰分析のエラーは正規分布に従うと考えます。
(28)式の仮定では、どの標本に関してもエラーは一定の分散の正規分布から発生します。しかし、【降水量】の多い日はエラーのばらつきが大きいなど、説明変数の大きさによってエラーの分散が異なる場合があります。こうした場合は、最小二乗法よりも精度が高い推定方法が存在します。また、最小二乗法の[推定係数の標準誤差]や[帰無仮説の検定結果]は不正確になります。『エラーは一定の分散の正規分布から発生するか?』という注意点があります。
実証分析の場合、真のエラー![]() は回帰分析の後でも分かりません。 このため、推定エラー
は回帰分析の後でも分かりません。 このため、推定エラー![]() から真のエラー
から真のエラー![]() を推測するしかありません。この確認として、推定エラー
を推測するしかありません。この確認として、推定エラー![]() と主な説明変数
と主な説明変数![]() や当てはめ値
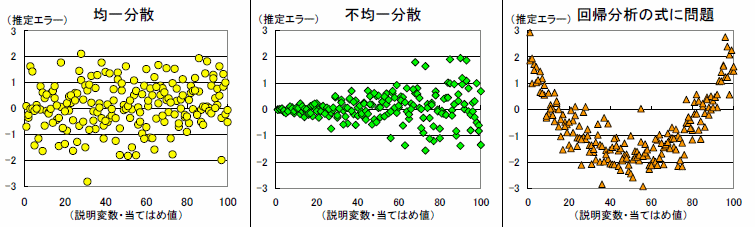
や当てはめ値![]() との散布図を描きます。 散布図が左下図のようになっていれば、エラーのばらつきは説明変数から影響を受けない均一分散と考えられます。一方、中央下図のようであれば、説明変数が増加するとエラーのばらつきが増える不均一分散であると考えられます。もし、右下図のようになっていれば、6.1 回帰分析の式の形や6.2 必要な説明変数の問題であると考えられます。
との散布図を描きます。 散布図が左下図のようになっていれば、エラーのばらつきは説明変数から影響を受けない均一分散と考えられます。一方、中央下図のようであれば、説明変数が増加するとエラーのばらつきが増える不均一分散であると考えられます。もし、右下図のようになっていれば、6.1 回帰分析の式の形や6.2 必要な説明変数の問題であると考えられます。
- Excelにおける回帰分析(最小二乗法)用乱数データのようなシミュレーションでは、
 のばらつきの大きさを設定でき、値を確認できます。
のばらつきの大きさを設定でき、値を確認できます。
- 時系列データなら、ダービン・ワトソン統計量
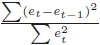 を使って検定することもあります。
を使って検定することもあります。
 |
この注意点に対する対処として、エラーの構造を指定する一般化最小二乗法やグループによってエラーの分散が異なるというランダム効果モデルを使うこともあります。 しかし、不均一分散がある場合に、通常の回帰分析(最小二乗法)を行っても深刻な問題は起きません。通常の回帰分析でも、現実に対応した推定係数を得ることができます。
- Excelの分析ツールでは、不均一分散に対応した推定はできません。
6.5 データの抜け落ち
快晴の日は傘屋が臨時休業してデータが抜けている可能性があります。また、傘の売れ行きが悪い場合、傘屋は回答を拒否するかもしれません。傘屋の状態や判断を通じた休業や回答拒否がある場合、回帰分析の結果は現実に対応しなくなる可能性があります。潜在データを含めた左下図の回帰線は、観測できるデータのみの右下図の回帰線とはっきりと異なっています。『回答やデータ作成に偏りのある抜け落ちがないか?』という注意点があります。
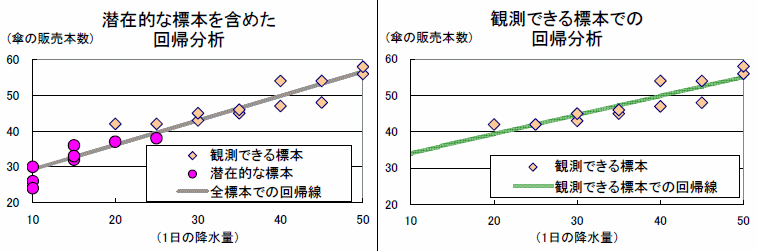
多くのケースでは、既に存在するデータを使うしかありません。回答やデータの作成プロセスで標本が偏る可能性がないかを考え、必要に応じて記述します。また、Heckit(ヘックマンの二段階推定)などのサンプルセレクションに対応した推定方法があります。ただ、サンプルセレクションに対応した推定方法は休業、無回答といった『この標本のデータが得られていない』という情報が必要です。
- サンプルセレクションに対応した推定では、データから抜け落ちる確率の変換値を説明変数として加えます。近似的な方法であればExcelの分析ツールでも実行できます。
6.6 データの正確さ
【傘の販売本数】が10本単位であったり、【降水量】が県単位の調査であったりとデータが不正確になっている場合があります。観測段階での測定誤差、データ公表段階での四捨五入や代表値、回帰分析の段階での代理変数など、複数の要因から回帰分析に用いるデータは不正確になります。『データは正確か?』という注意点があります。
被説明変数![]() が不正確であれば、推定エラーが大きくなり、推定精度が落ちます。しかし、現実と異なる推定係数になる傾向はありません。一方で説明変数
が不正確であれば、推定エラーが大きくなり、推定精度が落ちます。しかし、現実と異なる推定係数になる傾向はありません。一方で説明変数![]() が不正確であれば、右下図のように現実の関係を離れて推定係数が小さくなる傾向があります。説明変数が不正確である方がより深刻ですが、いずれの変数もできるだけ正確なデータを使ってください。
が不正確であれば、右下図のように現実の関係を離れて推定係数が小さくなる傾向があります。説明変数が不正確である方がより深刻ですが、いずれの変数もできるだけ正確なデータを使ってください。
- 説明変数の不正確さの大きさが分かれば、真の推定係数を見積もることができます。また、操作変数法を使うことでも対処できます。